How are we trackin'?
A "quick & dirty” estimate of the effective reproduction number of COVID-19
Originally posted 22 April 2020 at Pandemic Economics.
Let me introduce you to RPE, a “quick & dirty” estimate of the effective reproduction number of COVID-19.1
Today’s estimate of the effective reproduction number for COVID-19 in New Zealand is 0.11.
In a perfect world, the Government would be able to track the effective reproduction number (Reff) of COVID-19 on a daily basis. Reff is the average number of secondary infections per primary infection in an actual population given the policy measures in place at that time and the behavioural responses of that population.2 Tracking Reff allows the Government to both gauge the extent to which the virus is under control, and track the effects of changes to social distancing rules, or improvements in supporting measures such as testing, tracing and isolation.
RPE (estimates reproduction number), selected countries, 28 March - 22 April 2020
But accurate estimation of Reff requires complex modelling. So, I developed RPE – an easily calculated and updateable proxy measure of Reff (see below for the formula for RPE). I’ve calculated this proxy measure for the past three weeks for ten countries (including New Zealand) and for the states of Australia.3
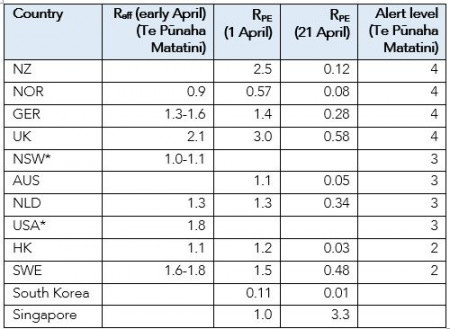
Te Pūnaha Matatini’s (Plank et al., 2020) reported estimates of Reff for six countries provides a useful crosscheck. So, I’ve compared RPE against Reff estimates from their complex model, finding a close match for most jurisdictions.
The following table compares estimates of RPE against Te Pūnaha Matatini’s estimates of Reff. Te Pūnaha Matatini did not specify a reference date for their estimates. The last New Zealand data point in their graphs is 5 April, suggesting a reference date in early April. Their Reff values are very close in most cases to RPE for 1 April.
[* I have not calculated RPE for NSW and the USA, as numbers of recovered individuals are not consistently available in the John Hopkins University dataset. Current RPE values for NSW are likely to be near zero as there have been very few new cases over recent days.]
In New Zealand, RPE fell quickly in response to the level 4 lockdown from 26 March. This fall is also apparent in all the comparator countries in this post, bar Singapore.4
An Reff below 1 corresponds to a situation in which the pool of infected individuals is shrinking, or equivalently, virus spread is under control. Acknowledging the imprecision of RPE, I propose a threshold of 0.8 rather than 1.
All countries in the graph bar Singapore are below the 0.8 threshold, that is, they have achieved effective control. How they have done so and how that might inform policy for New Zealand will be the subject of my next post.
I see value in RPE, or an equivalent measure, that can be updated daily. It could help decision makers monitor the success of policy measures to manage COVID-19 spread. New Zealand and other countries have made significant progress over the past few weeks (see graph). This makes it important to base policy on up-to-date data. RPE can help fill the gap between the less frequent, albeit more accurate, estimates of effective reproduction numbers for COVID-19 provided by the New Zealand Government’s modellers.
Calculation of RPE
RPE is calculated on a daily basis using the formula (new cases) / (active cases 5 days prior) * 10.
“5” in this equation is the assumed average number of days between infection and infectiousness (eg, Linton et al., 2020).
“10” is the average number of days an infected individual is infectious for. Following Siddarth and Weyl (2020), I assume individuals are no longer infectious 15 days after they became infected. This corresponds with the findings of Woelfel et al. (2020), who reported that people with COVID-19 but were not hospitalised had high levels of SARS-CoV-2 in their respiratory tract early on in their illness. The levels dropped off after four or five days of symptoms, and by the tenth day after they got sick, there was hardly any virus left. Zhou et al. (2020) reported that the virus was detectable in hospitalised patients in China for up to 20 days after symptoms started, but virus levels dropped off when symptoms did.
“Active cases” is the cumulative number of infected people less those recovered or died. To moderate the effects of data spikes, “new cases” and “active cases” are moving averages over three days.
High numbers of asymptomatic infectious individuals, if present, would bias RPE downwards. This becomes more problematic for the model as the numbers decline and we get very few new positive cases.
References
Delamater, P. L., Street, E. J., Leslie, T. F., Yang, Y., & Jacobsen, K. H. (2019). Complexity of the Basic Reproduction Number (R0). Emerging Infectious Diseases, 25(1), 1-4. https://dx.doi.org/10.3201/eid2501.171901
Linton, N. M., Kobayashi, T., Yang, Y., Hayashi, K., Akhmetzhanov, A. R., Jung, S., Yuan, B., et al. (2020). Incubation Period and Other Epidemiological Characteristics of 2019 Novel Coronavirus Infections with Right Truncation: A Statistical Analysis of Publicly Available Case Data. Journal of Clinical Medicine, 9(2), 538. MDPI AG. http://dx.doi.org/10.3390/jcm9020538
Plank, M.J., Binny, R.N., Hendy, S.C., Lustig, A., James, A., & Steyn, N. (9 April 2020) A stochastic model for COVID-19 spread and the effects of Alert Level 4 in Aotearoa New Zealand. https://www.medrxiv.org/content/10.1101/2020.04.08.20058743v1.full.pdf
Siddarth, D., & Weyl, E.G. (2020). Why We Must Test Millions a Day. COVID-19 Rapid Response Impact Initiative, White Paper 6. Edmond J. Safra Center for Ethics. https://ethics.harvard.edu/files/center-for-ethics/files/white_paper_6_testing_millions_final.pdf
Woelfel, R., Corman, V.M., Guggemos, W., Seilmaier, M., Zange, S., et al. (2020). Clinical presentation and virological assessment of hospitalized cases of coronavirus disease 2019 in a travel-associated transmission cluster. [Preprint]. https://doi.org/10.1101/2020.03.05.20030502
Zhou, F., Yu, T., Du, R., Fan, G., Liu, Y., et al. (2020). Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. The Lancet. 395(10229), p. 1054-1062. https://doi.org/10.1016/S0140-6736(20)30566-3
Data
Data from John Hopkins University downloaded 13:30 17 April 2020 NZST. This includes NZ data up to 16 April. https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series
Notes
1. “PE” in RPE stands for “Proxy Estimate”.
2. Reff is the effective reproduction number at a point in time in an actual population, given actual control measures in place and behavioural responses by that population. It differs from the commonly citied reproduction numbers R0 and Re. R0 is the number of secondary cases one primary case would produce in a completely susceptible population (Delamater et al., 2019). Re is the average number of secondary cases per infectious case in a population made up of both susceptible and non-susceptible hosts. R0, Re and Reff will typically be the same at the onset of a pandemic, but will diverge over time.
3. This graph could easily be extended to many more countries and further into the past. The calculation is only as good as the quality of the underlying data, making it less reliable for developing countries. RPE assumes closed borders (or that the net movement of infected individuals across borders is small relative to the number of active cases). It does not make sense to apply the model to periods when a major source of infection is people arriving from other countries.
4. The countries in this note are based on the list in Plank et al. (2020). That paper presents estimates of Reff in these countries drawn from a forthcoming paper by Binny et al. I added South Korea and Singapore as interesting edge cases – South Korea because they brought the number of new cases down to low numbers in March, and Singapore as its virus control performance has recently deteriorated.